A számsorok derivációja? - Derivation of number order?
Itt egy olyan módszert írok le, mely nagyon könnyen használható, ha bizonyos számsorban valamilyen összefüggést szeretnénk megtalálni. (Természetesen csak bizonyos típusú összefüggésekre alkalmazható ez az eljárás, amiről itt most nem írok bővebben.)
Lineáris összefüggés
Vegyünk egy egyszerű számsort: y=f(x); y=3x+5

Ha nem ismerjük az összefüggést, csupán egy számsort látunk, és szeretnénk megtalálni az összefüggést, akkor ezt nagyon egyszerű módon megtehetjük.
Először vizsgáljuk meg a középpont szerinti szimmetriát: 8+29, 11+26, 14+23, 17+20, …
Minden esetben a számok összege azonos, ami azt jelenti, hogy lineáris összefüggésről van szó.
Most vizsgáljuk meg a szomszédos számok közti eltéréseket: 11-8, 14-11, 17-14, 20-17, 23-20, 29-26.
Minden esetben az eredmény 3, hiszen a f(x)=3x+5 függvény derivációja f’(x)=3.
Ha a sorozatból levonjuk a 3x értékeket, megkapjuk az 5 értékű konstanst is.
Polinomiális összefüggés

Itt a középpont szerinti szimmetriát alkalmazva a számok összege már nem konstans, tehát nem lineáris összefüggésről van szó.
Vegyük tehát a szomszédos számok közti eltéréseket:

A középpont szerinti szimmetria: 9+41, 13+37, 17+33, … értéke mindenhol azonos, tehát már lineáris összefüggésről van szó.
A számok közti eltérés mindenhol azonos: 13-9, 17-13, … = 4, hiszen 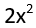 derivációja 4x.
Miután levonjuk a számsorból ezt a kvadratikus sorozatot, megkapjuk a lineáris sorozatot, amit már az előzőek alapján meg lehet oldani.
derivációja 4x.
Miután levonjuk a számsorból ezt a kvadratikus sorozatot, megkapjuk a lineáris sorozatot, amit már az előzőek alapján meg lehet oldani.
Mivel a második szinten értük el a lineáris függvényt, ezért a számsort egy kvadratikus függvénnyel lehet leírni: 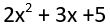
Exponenciális összefüggés


A megkapott számsorból újra kiszámoljuk a szomszédos számok közti különbséget, de ahogy láthatjuk a számsor sohasem végződik, illetve nem jutunk lineáris összefüggéshez.

Azt is mondhatjuk, hogyha N+1 szám közti összefügést akarjuk megtalálni, akkor nem alkalmazhatunk egy N-ed rendű polinomot, mert azzal nem redukálnánk a bonyolultságot (tehát valójában semmilyen összefüggést nem állapítanánk meg).
Fel kell tételeznünk, hogy exponenciális függvénnyel van dolgunk, hiszen egy exponenciális függvény derivációja szintén exponenciális függvény lesz.
A kapott sorozatokban vizsgáljuk meg a szomszédos számok osztásának eredményeit:

Ebből jól láthatjuk, hogy ez a sorozat gyorsan közelít a 3 értékhez, ami a függvényben a 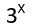 tagnak felel meg.
tagnak felel meg.
A 3 itt még nem pontos, mivel még néhány derivációt el kell végezni ahhoz, hogy a polinomiális rész ne legyen hatással az eredményre, ahogy azt a lenti táblázat is mutatja.
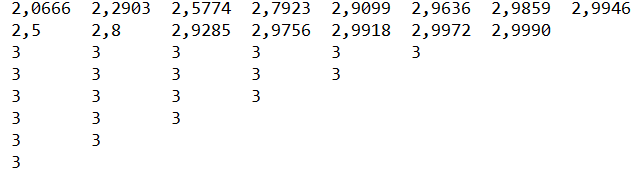
Mindez azt jelenti, hogy végső soron "lineáris összefüggésre vezettük vissza" a sorozatot.
Megjegyzés:
Ha például 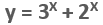 függvény számsorát használnánk, akkor szintén először megkapnánk a 3-értéket, ez szerint a metódus szerint. Miután levontuk a függvényből a
függvény számsorát használnánk, akkor szintén először megkapnánk a 3-értéket, ez szerint a metódus szerint. Miután levontuk a függvényből a 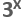 tagot,
utána megkapnának
tagot,
utána megkapnának 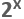 tagot, ez szerint a metódus szerint . Viszont, ebben az esetben már 10-nél jóval több mérési értékre lenne szükségünk ahhoz, hogy ez a numerikus metódus megfelelő pontossággal tudjon működni.
tagot, ez szerint a metódus szerint . Viszont, ebben az esetben már 10-nél jóval több mérési értékre lenne szükségünk ahhoz, hogy ez a numerikus metódus megfelelő pontossággal tudjon működni.
A számsorok derivációja? - Derivation of number order?
Itt egy olyan módszert írok le, mely nagyon könnyen használható, ha bizonyos számsorban valamilyen összefüggést szeretnénk megtalálni. (Természetesen csak bizonyos típusú összefüggésekre alkalmazható ez az eljárás, amiről itt most nem írok bővebben.)
Lineáris összefüggés
Vegyünk egy egyszerű számsort: y=f(x); y=3x+5

Ha nem ismerjük az összefüggést, csupán egy számsort látunk, és szeretnénk megtalálni az összefüggést, akkor ezt nagyon egyszerű módon megtehetjük.
Először vizsgáljuk meg a középpont szerinti szimmetriát: 8+29, 11+26, 14+23, 17+20, …
Minden esetben a számok összege azonos, ami azt jelenti, hogy lineáris összefüggésről van szó.
Most vizsgáljuk meg a szomszédos számok közti eltéréseket: 11-8, 14-11, 17-14, 20-17, 23-20, 29-26.
Minden esetben az eredmény 3, hiszen a f(x)=3x+5 függvény derivációja f’(x)=3.
Polinomiális összefüggés

Itt a középpont szerinti szimmetriát alkalmazva a számok összege már nem konstans, tehát nem lineáris összefüggésről van szó.
Vegyük tehát a szomszédos számok közti eltéréseket:

A középpont szerinti szimmetria: 9+41, 13+37, 17+33, … értéke mindenhol azonos, tehát már lineáris összefüggésről van szó.
A számok közti eltérés mindenhol azonos: 13-9, 17-13, … = 4, hiszen 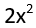 derivációja 4x.
derivációja 4x.
Mivel a második szinten értük el a lineáris függvényt, ezért a számsort egy kvadratikus függvénnyel lehet leírni: 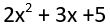
Exponenciális összefüggés


A megkapott számsorból újra kiszámoljuk a szomszédos számok közti különbséget, de ahogy láthatjuk a számsor sohasem végződik, illetve nem jutunk lineáris összefüggéshez.

Azt is mondhatjuk, hogyha N+1 szám közti összefügést akarjuk megtalálni, akkor nem alkalmazhatunk egy N-ed rendű polinomot, mert azzal nem redukálnánk a bonyolultságot (tehát valójában semmilyen összefüggést nem állapítanánk meg).
Fel kell tételeznünk, hogy exponenciális függvénnyel van dolgunk, hiszen egy exponenciális függvény derivációja szintén exponenciális függvény lesz.
A kapott sorozatokban vizsgáljuk meg a szomszédos számok osztásának eredményeit:

Ebből jól láthatjuk, hogy ez a sorozat gyorsan közelít a 3 értékhez, ami a függvényben a 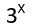 tagnak felel meg.
tagnak felel meg.
A 3 itt még nem pontos, mivel még néhány derivációt el kell végezni ahhoz, hogy a polinomiális rész ne legyen hatással az eredményre, ahogy azt a lenti táblázat is mutatja.
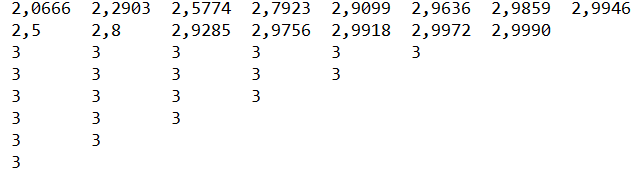
Mindez azt jelenti, hogy végső soron "lineáris összefüggésre vezettük vissza" a sorozatot.
Megjegyzés:
Ha például 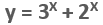 függvény számsorát használnánk, akkor szintén először megkapnánk a 3-értéket, ez szerint a metódus szerint. Miután levontuk a függvényből a
függvény számsorát használnánk, akkor szintén először megkapnánk a 3-értéket, ez szerint a metódus szerint. Miután levontuk a függvényből a 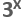 tagot,
utána megkapnának
tagot,
utána megkapnának 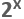 tagot, ez szerint a metódus szerint . Viszont, ebben az esetben már 10-nél jóval több mérési értékre lenne szükségünk ahhoz, hogy ez a numerikus metódus megfelelő pontossággal tudjon működni.
tagot, ez szerint a metódus szerint . Viszont, ebben az esetben már 10-nél jóval több mérési értékre lenne szükségünk ahhoz, hogy ez a numerikus metódus megfelelő pontossággal tudjon működni.






 Menu
Menu Új írások
Új írások 








