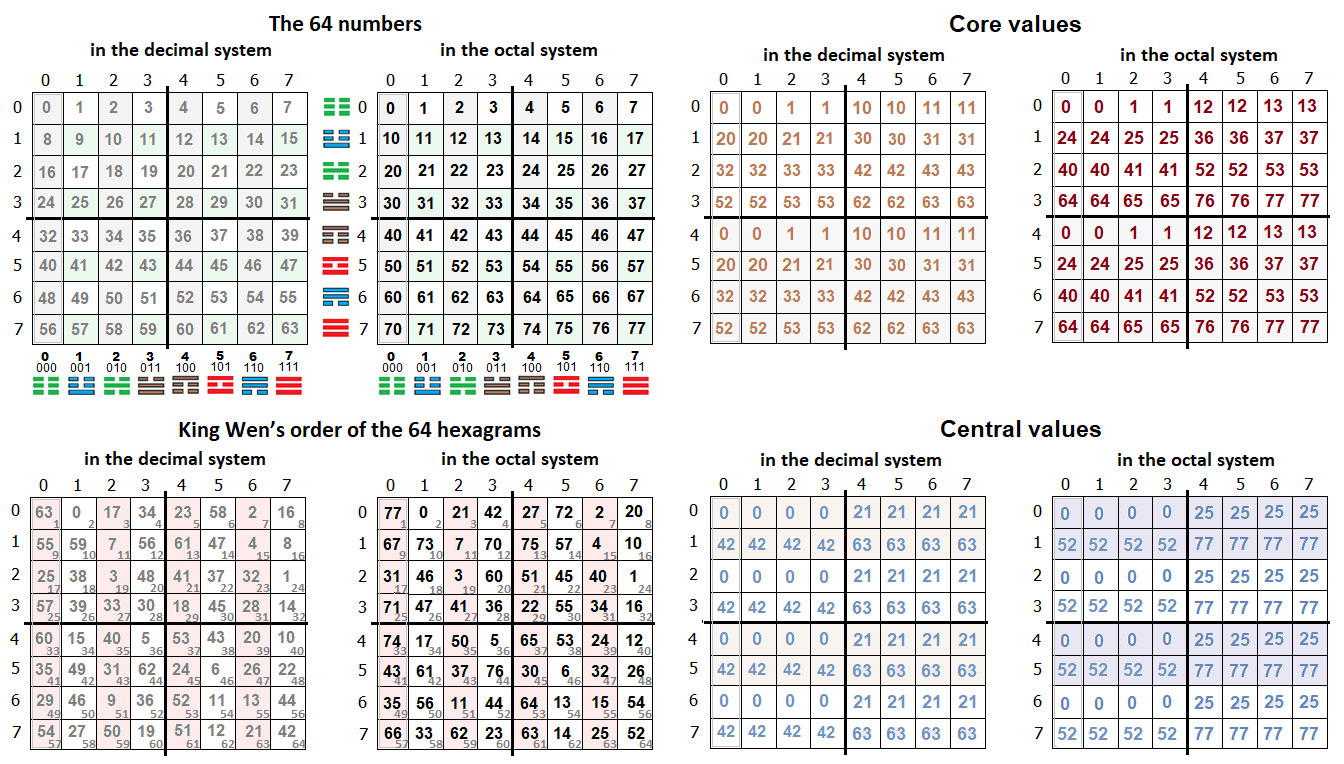
A hexagramok felosztása

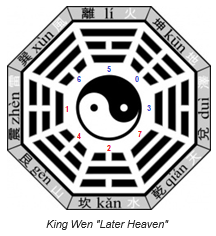
A I-Ching legősibb iratai közé tartozik Wen királynak tulajdonított 64 hexagram.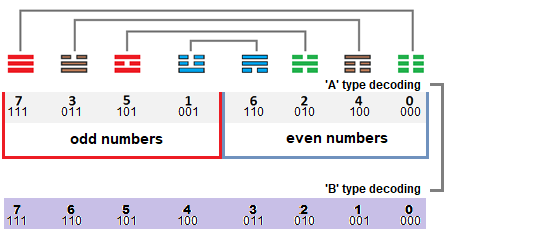 Fuxi elrendezése ugyan ősibb, de minden bizonnyal Wen király volt az, aki először létrehozta a nyolc trigramokból a 64 hexagramot. A 32 pár hexagram általában mindig ugyanabban sorrenden szerepel az ősi iratokban, ezért ezt a sorrendet kanonikus sorrendnek nevezzük, (lásd a linkeket: [0], [1]).
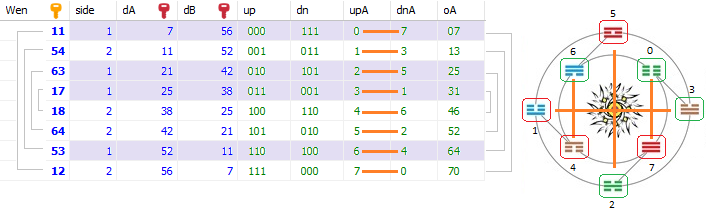
A mellékelt képen a trigramok szimmetriái láthatók és azok számértékei, kétféle dekódolás szerint:"A type decoding (dA)" és "B type decoding (dB)", attól függően, hogy alulról vagy felülről olvassuk a trigramot.

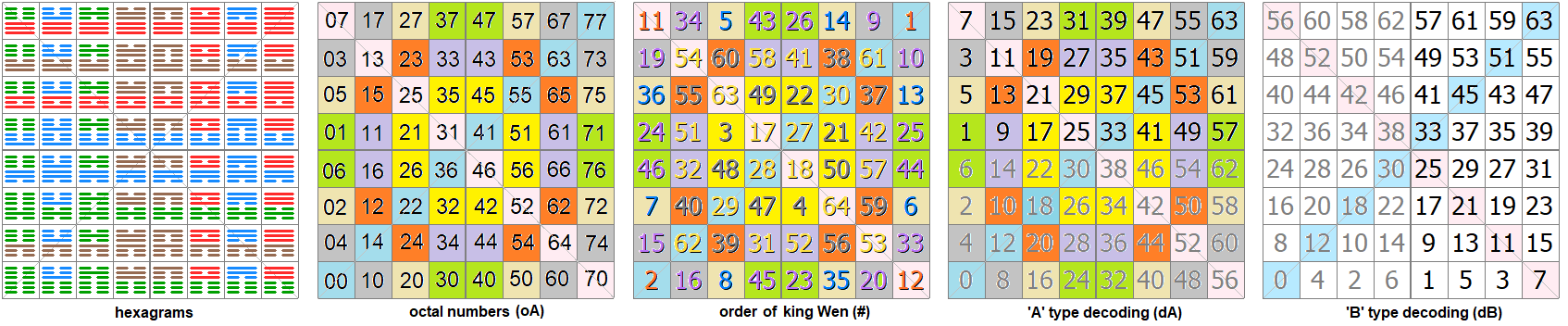
Ebben a leirásban a hexagramok nyolcas (oktális) számrendszer szerinti értékét _oA is használni fogjuk. Ennek az az előnye, hogy a számban látható a hexamot alkotó két trigram értéke is.
Példul a 37_oA hexagram: fent a 3 és lent a 7 trigram. A 77_oA hexagramot a 7 és 7 trigramok alkotják, ami tízes számrendszerben 63_dA és Wen király számozásában az első 1_Wen hexagram.
Ha a 37_oA hexagram trigramjait felcseréljük, akkor a 73_oA hexagramot kapjuk. (73_oA = 7*8+3 = 59_dA ertekű a tízes, dekadikus számrendszerben.)
A 37_oA hexagram bináris negációja a 40_oA hexagram lesz, mivel a 3 bináris negációja 4 _(7-3=4) és a 7 negációja 0, ahogy az fenti képen látható.
A 37 hexagram megfordítása a tigramok megfordítása és felcserélése, tehát 37_oA hexagram megfodítása 71_oA hexagram lesz. Tehát a nyolcas számrenszerben rögtön látjuk a hexagram két trigramját és könnyen meghatározhatjuk a hexagram bináris negációját is, ezért jóval kifelyezőbb, mint a hexagram értéke a tízes számrendszerben.

A hexagramok felosztása

A 32 pár felosztható két nagy csoportra:
1. 8 pár "speciális" vagy "diagonális". (A szakirodalomban "speciális" hexagramok néven ismertek.)
A 192 szimmetrikus elrendezésben mindig a diagonálisokon találhatók, kék és piros színnel jelölve (ezért kapták a "diagonális" nevet).

2. A maradék 24 pár "nem speciális" vagy "nem diagonális".

A diagonális hexagramok még feloszthatók két csoportra, melyek egymásra merőlegesek.
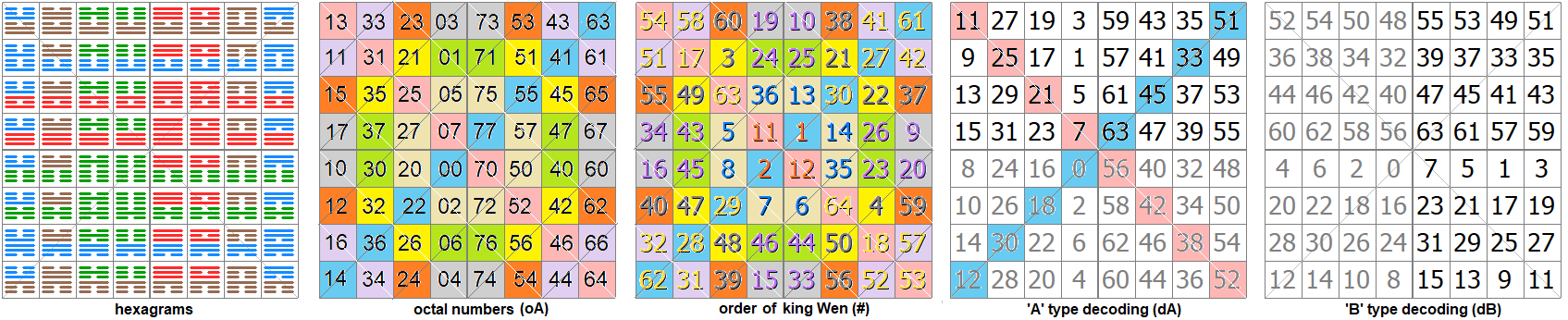
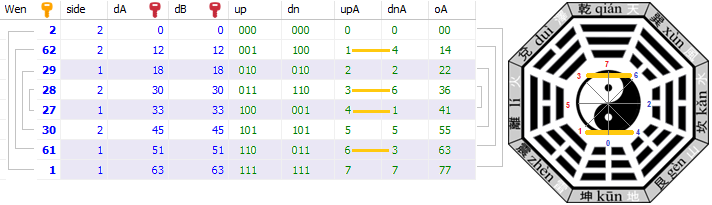
Ahhoz, hogy lássuk ezt a merőlegességet, a 192 szimmetrikus elrendezésből egy esetet mutatok be a jobb vizuális megértés érdekében:

1.1. A diagonális hexagramok első csoportja, ahol "A type decoding" értéke egyenlő "B type decoding" értékkel, tehát dA = dB .
Ezeknél a hexagramoknál a felső és az alsó trigram egymás tükörképei. A 192 szimmertriában kék színnel vannak jelölve a diagonálison. Itt érvényes, hogy a számok összege ∑ dA = 4 x 63 .
Ezek: [2, 62, 29, 28, 27, 30, 61, 1]_Wen = [00, 14, 22, 36, 41, 55, 63, 77]_oA = [0, 12, 18, 30, 33, 45, 51, 63]_dA
Ez a csoport még felosztható két részre az szerint, hogy a felső és az alsó trigram megegyezik a hexagramban vagy nem.

1.2. A diagonális hexagramok második csoportja, ahol dA + dB = 63 .
Ezeknél a hexagramoknál a felső és az alsó trigram egymás tükörképének a negációja. A 192 szimmertriában piros színnel vannak jelölve a diagonálison. Itt is érvényes, hogy a számok összege ∑ dA = 4 x 63 .
Ha jól megfigyeljük ez a szimmetria valójába Wen király pakuája, de nem a trigramok hanem már a hexagramok szintjén.
Ez a szimmetria tökéletesen bizonyítja Wen kirány pakuájának helyességét.
Ezek: [11, 54, 63, 17, 18, 64, 53, 12]_Wen = [07, 13, 25, 31, 46, 52, 64, 70]_oA = [7, 11, 21, 25, 38, 42, 52, 56]_dA
Ez a csoport is felosztható két részre az szerint, hogy a felső és az alsó trigram egymás bináris negációja vagy nem.

Látva ezen szimmetriákat észre kell venni, hogy teljesen mindegy milyen dekódolást választunk, hogy a hexagram megszakított vonala nulla vagy egyes lesz, illetve alulról vagy felülről olvassuk a hexagramokat, mert ez a rendszer független a dekódolástól. Ez azt jelenti, ha más dekódolást választunk, akkor is kijönnek ezek az összefüggések, csupán más számok lesznek a táblázatokban. Tehát felesleges arról vitatkozni, hogy milyen matematikai dekódolás a helyes, és melyik a helyes olvasat, mert teljesen mindegy. Ez csak megegyezés kérdése, de a lényegen semmit nem változtat. Ebből is szépen látható a régi mesterek bölcsessége.

2.1 A 24 nem diagonális pár felosztása
A 24 nem diagonális pár felosztása már egy kicsit nagyobb fejtörést okozott számunkra, de a végeredmény mégis egyszerű lett. Több módon is levezettük ezt a felosztást, itt a legegyszerűbb megoldást közlöm le.
A nem diagonális hexagramok feloszthatók 6 logikus csoportra. Minden csoport 8 elemet tartalmaz, színekkel jelölve. Itt is minden csoportban érvényes, hogy a számok összege ∑ dA = 4 x 63 , mint a diagonális hexagramoknál. Ennek ilusztrálására a 192 szimmetrikus elrendezésből egy példán szinekkel jelöltük az egyes csoportokat.

A lenti ábrán a 6 csoportból az egyik van kiemelve.
Két egyforma nagyságú, de egymásra merőlegesen elhelyezett téglalap sarkain lévő 8 hexagram alkot egy csoportot.

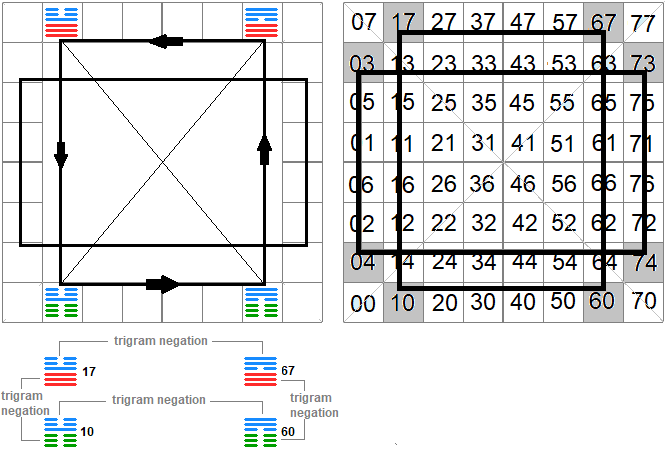
A nem diagonális hexagramok 6 csoportja:
1. [34,20,16,09 - 10,15,19,33]_Wen = [17,60,10,67 - 73,04,03,74]_oA = [15,48,08,55 - 59,04,03,60]_dA , szürke
2. [45,43,26,23 - 24,25,44,46]_Wen = [30,37,47,40 - 01,71,76,06]_oA = [24,31,39,32 - 01,57,62,06]_dA , zöld

3. [49,47,22,04 - 03,21,48,50]_Wen = [35,32,45,42 - 21,51,26,56]_oA = [29,26,37,34 - 17,41,22,46]_dA , sárga
4. [60,56,39,38 - 37,40,55,59]_Wen = [23,54,24,53 - 65,12,15,62]_oA = [19,44,20,43 - 53,10,13,50]_dA , narancs

5. [35,14,08,05 - 06,07,13,36]_Wen = [50,57,20,27 - 72,02,75,05]_oA = [40,47,16,23 - 58,02,61,05]_dA , krém
6. [58,52,41,31 - 32,42,51,57]_Wen = [33,44,43,34 - 16,61,11,66]_oA = [27,36,35,28 - 14,49,09,54]_dA , lila

Ezekben a csoportokban minden hexagramra igaz, hogy a hexagram "Later Heaven" párja ugyan ebben a csoportban van. (A "Later Heaven" kapcsolat a hexagram megfordítása és bináris negaciója, ahogy azt már korábban levezettük.)
A szürke (1.) csoportban szereplő hexagramok trigramjainak a felcserélései a zöld (2.) csoportban vannak (17-71, 60-06, 10-01, ...).
A sárga (3.) csoportban szereplő hexagramok trigramjainak a felcserélései a narancs színű (4.) csoportban vannak.
A krém (5.) színű csoportban szereplő hexagramok trigramjainak a felcserélései ugyan ebben a csoportban vannak.
A lila (6.) csoportban szereplő hexagramok trigramjainak a felcserélései szintén ugyan ebben a csoportban vannak, de ez az egyetlen csoport, ahol olyan hexagramok is szerepelnek melyeknek alsó és a felső trigramjai megegyeznek.
Ami még érdekes ezekkel a csoportokkal kapcsolatban:
  A lila (6.) csoportban csak a föld elemnek (3, 4) és a levegő elemnek (1, 6) megfelelő trigramok szerepelnek a hexagramokban.
  A krém (5.) csoportban csak a tűz elemnek (5, 7) és a víz elemnek (2, 0) megfelelő trigramok szerepelnek a hexagramokban.
  A sárga (3.) és a narancs (4.) csoportokban nincs 7 és 0 trigram a hexagramokban.
  A szürke (1.) és a zöld (2.) csoportokban nincs 5 és 2 trigram a hexagramokban.

Még két fontos dolgot érdemes tudni a hexagramokról:
1. A hexagram mag értéke (core or nuclear hexagram) [3], [4]
2. A hexagram centrális értéke, ami nem más mit a mag hexagramból újra létrehozott mag érték, ismételve a műveleteket.

Ha megvizsgáljuk a 192 szimmetrikus elrendezést, akkor észre vehetjük, 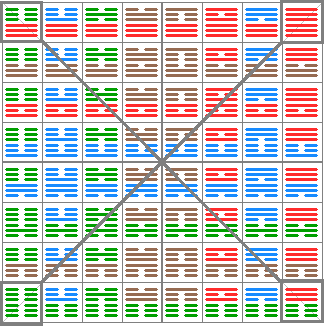hogy [1,2]_Wen hexagramok minden esetben meghatározzák a [11,12]_Wen hexagramok elhelyezkedését is (minden esetben egymásra merőleges elhelyezkedésűek, természetesen a megfelelő sor és oszlop figyelembevételével). Ez igaz minden duális párra a kék diagonálison. A kék diagonális duális párjai, meghatározzák a piros diagonális duális párjait is, minden esetben merőlegsséget hozva létre.
[01,02]_Wen : [11,12]_Wen = [77,00]_oA : [07,70]_oA = [63,0]_dA : [56,7]_dA
[27,28]_Wen : [17,18]_Wen = [41,36]_oA : [31,46]_oA = [33,30]_dA : [25,38]_dA
[30,29]_Wen : [63,64]_Wen = [55,22]_oA : [25,52]_oA = [18,45]_dA : [21,42]_dA
[61,62]_Wen : [53,54]_Wen = [63,14]_oA : [13,64]_oA = [51,12]_dA : [11,52]_dA
Tehát egy diagonális hexagram (ezen összefüggések alapján) még 3 másik hexagramot határoz meg (négyes szimmetria). Ez azt jelenti, hogy 4 diagonalis eleme 4 pozicióban 16 lehetséges elrendezését adja a diagonális elemeknek. Mivel összesen 192 szimmetrikus elrendezés van, ezért a 6 nem diagonlis csoport 12 féle elrendezést genegál, mert 12x16=192.

Összegezve a hexagramok nyolc csoportja (növekvő érték szerint rendezve a hexagramokat a csoportokban):
1. 8 pár "speciális" vagy "diagonális":
 [02,29,30,01 - 62,28,27,61]_Wen = [00,22,55,77 - 14,36,41,63]_oA = [00,18,45,63 - 12,30,33,51]_dA, kék
 [11,63,64,12 - 54,17,18,53]_Wen = [07,25,52,70 - 13,31,46,64]_oA = [07,21,42,56 - 11,25,38,52]_dA, piros

2. A maradék 24 pár "nem speciális" vagy "nem diagonális":
 [16,34,20,09 - 19,15,10,33]_Wen = [10,17,60,67 - 03,04,73,74]_oA = [08,15,48,55 - 03,04,59,60]_dA , szürke
 [45,43,23,26 - 24,46,25,44]_Wen = [30,37,40,47 - 01,06,71,76]_oA = [24,31,32,39 - 01,06,57,62]_dA , zöld

 [47,49,04,22 - 03,48,21,50]_Wen = [32,35,42,45 - 21,26,51,56]_oA = [26,29,34,37 - 17,22,41,46]_dA , sárga
 [60,39,38,56 - 40,55,59,37]_Wen = [23,24,53,54 - 12,15,62,65]_oA = [19,20,43,44 - 10,13,50,53]_dA , narancs

 [08,05,35,14 - 07,36,06,13]_Wen = [20,27,50,57 - 02,05,72,75]_oA = [16,23,40,47 - 02,05,58,61]_dA , krém
 [58,31,41,52 - 51,32,42,57]_Wen = [33,34,43,44 - 11,16,61,66]_oA = [27,28,35,36 - 09,14,49,54]_dA , lila

Megjegyzés: A csoportok színei teljesen véletlenszerűen voltak kiválasztva, tehát a színek és az egyes csoportok közt nem kell keresni semmilyen rejtett összefüggést.